지난 표면(surface)에 관한 글에 이어 표면에너지(surface energy)를 시작합니다. 날이 조금 시원해지긴 했어도 제방은 바람이 안통해서 후끈합니다. ㅠ_ㅠ 그러니 가능한 간단하게. 아주 간단하게 갑시다. - _-
표면이란 무엇인가를 이야기할때, 최외각층 원자, 최외각 분자층, 그리고 화학반응이 일어나는 층 등 몇가지 관점이 있었습니다. 그렇다면 표면에너지도 과연 그렇게 몇가지로 구분을 해야하나 하는 의문이 생길 수 있겠죠. 하지만 걱정없는 것이 표면에너지는 한가지만 고려해도 됩니다. 바로 '최외각원자' 가 그 주인공입니다. 오늘의 주인공인 이쁘장한 최외각층 원자를 다시한번 자세히 봅시다.

물체의 단면을 잘랐을때, 나란히 배열된 원자들.
위 그림은 어느 물질을 자른 단면에서 원자들이 어떻게 위치해 있는지 원자 배열을 간략하게 나타낸 것 입니다. 붉은 색으로 표현된것들이 최외각층 원자이고, 밝은 파란색은 내부 원자가 되겠죠. 여기서 최외각층 원자는 내부 원자와 확연히 다른 한가지 차이점이 있습니다. 각각의 내부원자들은 주위 원자들과 결합을 하고 있는데, 'B'로 표기된 내부원자를 보면 상하좌우 모두 4개의 원자와 결합을 하고 있습니다. 그런데 최외각층 원자 'A'를 보면 바로 위에 있어야 할 원자 하나가 없어서 3개의 원자와만 결합을 하고 있습니다. 원자끼리 결합을 하기 위해서는 원자의 종류마다 다르지만 특정한 에너지를 필요로 하며, 우리는 그것을 '결합에너지' 라고 부릅니다. 내부 원자인 B는 원자 1개당 4개까지 결합을 할 수 있는 능력이 있는데, 최외각 원자인 A는 3개만 결합을 하고있고, 1개는 결합을 못하고 있습니다. 이렇게 결합을 하지 못하고 있는 부분을 broken bond(또는 dangling bond) 라고 하는데, broken bond 1개는 원자 1개와 더 결합할 수 있는 여분의 에너지(extra energy)를 갖고있습니다. 이 여분의 에너지는 최외각원자 1개당 1개씩 갖고 있으므로, 물질 전체로 본다면 표면에 존재하는 최외각원자 수 만큼 존재하게 됩니다. 바로 이 원자들의 여분 에너지를 모두 합한 (여분 에너지 x 최외각원자 수)를 흔히 '표면에너지' 라고 부릅니다.

원자 배열이 민망하게 쬐까 다른 경우
이제는 원자들의 배열이 조금 다른 경우을 한번 살펴봅시다. 위 그림에서 내부원자 'B' 는 좌우로 1개씩, 아래에 대각선 방향으로 좌우 각각 1개씩, 위쪽도 대각선 방향으로 각각 1개씩 결합하고 있습니다. 그래서 1개의 내부 원자는 모두 6개의 주위 원자들과 결합을 하고있죠. 그리고 'A' 라고 표기된 최외각원자를 보면, 위쪽 좌우 대각선 방향으로 결합해 있어야 할 2개의 원자들이 없습니다. 그래서 최외각 원자 1개당 broken bond는 2개가 되고, 여분의 결합에너지도 2배가 됩니다. 단순히 산술적으로만 보면 앞의 최외각원자 1개당 1개의 여분 에너지를 가졌던 것에 비하여 표면에너지가 2배 크다는 이야기가 되는데요, 이것은 아주 중요한 의미를 내포합니다. 똑같은 물질이라도 원자가 결합한 각도나 방향에 따라, 다시 말하면 우리가 어떤 방향에서 보느냐에 따라 표면 에너지가 모두 다르다는 것을 말해주기 때문입니다. '기판의 선택과 세척'( http://marriott.tistory.com/113 ) 이야기를 할 때, Si wafer 종류에 (100), (111) 방향의 특성이 서로 다르기 때문에 원하는 것을 골라써야 한다는 말을 기억하실 겁니다. 바로 이러한 이유 때문에 그렇습니다.

Cubic 결정구조에서 (100), (111), (110) 면. 요즘 그림에 3D 는 기본.
결정구조가 뭐냐고 물으시면, 대답하는데 2개월은 걸립니다.
그러니 묻지마세요 - _- 물어도 대답안함 -_-
물질을 구성하는 원자들은 각각의 특정한 결정구조를 갖고 있습니다. 그런데 같은 물질이라도 우리가 보는 방향에 따라 원자들의 배열 형태가 달라지기 때문에, 물질을 어느 방향으로 자르냐에 따라 표면에너지가 모두 달라집니다. 그럼 심심하기도 하니 -_ - FCC(Face Centered Cubic) 결정구조에서 (100), (111), (110) 면들의 표면에너지가 얼마나 차이가 나나 한번 비교해 보겠습니다. 먼저 (100) 면의 표면 에너지 입니다. 그런데 정말 어째 무슨 교과서에나 나오는 심심한 내용이 될지도 모르겠군요 -_ -

FCC 결정구조에서 (100)면의 표면 원자배열
오늘 그림이 칼라풀 하지가 않아..
이제부터 '최외각 원자'를 '표면 원자' 라고 부르도록 하겠습니다. 위 (100)면의 그림에서 표면 원자중 A 원자 하나만 봅시다. 이 원자는 2차원적으로 보게되면 4개의 주변 원자와 결합을 하고 있게 됩니다. 그럼 이걸 3차원으로 확장을 해봅시다. 박막을 만든다는 것은 기존의 표면위에 원자층을 올려서 새로운 표면을 만드는 작업이라고 했습니다. 그래서 저 표면원자들 위에 다른 원자들을 쌓아올리는 거죠. 그런데 원자들은 아무데나 자리할 수 있는게 아니라, 각각의 면 방향에 따라 일정한 규칙성을 가지고 자리를 잡습니다. 바로 원자들과 원자들 사이의 가장 큰 빈 공간에 우선적으로 들어가게 됩니다. 그게 가장 쉽고 안정하니까요. 그래서 A 원자 위쪽 주변 빈 공간에 하나씩 모두 4개의 원자가 들어가게 되고, 그런 이유로 (100)면의 표면원자 하나는 4개의 끊어진 결합에너지(여분 에너지)를 가집니다.

요롷게.. A 원자 위의 빈 공간에 4개가 살포시 즈려밟는다.
그런데 여기서 하나 고려해야 할 것이 있습니다. 원자와 원자간의 결합이 끊길때, 결합에너지는 어느 원자 하나가 모두 가져가는 것이 아니라 서로가 반씩 나눠갖게 됩니다. 그래서 원자간의 결합에너지를 ε 라 하면, 결합이 끊어진 후 한쪽 원자가 가진 결합에너지는 ε/2 가 되고, (100)면의 표면 원자 하나당 갖고있는 표면에너지는 (ε/2 x 4) 가 되는 겁니다. 물론 이 값은 대략적인 값입니다. 표면에너지는 가장 표면원자 뿐 아니라 두번째 표면원자, 세번째 표면원자 등도 어느정도 영향을 주게 되는데(표면에너지 #2 참조), 이러한 것들을 고려하지 않았기 때문입니다.

두 원자 사이의 결합에너지를 ε 라 하면,
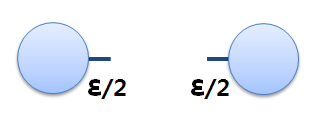
결합이 끊어진 뒤,
원자 하나당 1/2 ε의 에너지가 남게됨
이번에는 FCC 구조에서 최대조밀면이라고 하는 (111)면을 살펴보겠습니다. (111)면의 표면 원자들은 원자 하나에 6개가 둘러싸고 있습니다. 그리고 A 의 표면원자 위로 원자가 들어갈 수 있는 빈 공간은 3개 뿐 입니다. 즉, 원자 하나당 끊어진 결합은 3개가 존재하고, (111)면의 원자 하나당 표면 에너지는 (ε/2 x 3) 이 됩니다. (100)면의 원자보다 에너지가 낮습니다.

FCC에서 (111) 면의 표면 원자 배열

요로코롬.. A 원자 위 빈자리에 3개가 살포시 내려앉는다
그럼 마지막으로 (110)면을 보겠습니다. 이 면은 다른것들에 비해 층의 모양이 확연하게 구분이 됩니다. 좌우로는 결합해 있지만, 위-아래로는 결합한 것들이 없이 모두 끊어져 있습니다. 그렇다면 이 방향에서는 A 원자 하나가 과연 몇개의 원자와 결합하고, 그 원자들은 어떤 위치에 자리잡고 있을까요. (100), (111) 면도 그렇지만, (110)면에서는 FCC라는 결정이 어떻게 생겼는지 결정구조를 정확히 알지 못하면 원자의 위치를 이해하기가 쉽지 않습니다. FCC 구조를 머리속에서 3차원으로 그려서 빙글빙글 돌릴 수 있어야 하죠. 그러나 비록 위치는 몰라도 몇개인지 알아내는것은 아주 간단합니다. FCC 결정에서 원자들의 위치를 3차원으로 정확히 그려내지 못한다 해도, 결정구조를 배운 사람이라면 FCC의 배위수(원자 하나당 결합하고 있는 원자수)는 12개라는 것은 알고 있을 겁니다. 그것만 알면 됩니다.

이거슨 FCC에서 (110)면 표면 원자 배열
좌우로 하나씩만 결합해 있다. 나머지는?
자, FCC 결정을 이루고 있는 원자는 어느것이든 12개의 주위 원자와 결합합니다. 앞의 (100)면의 예를 보면, 처음에 A 원자는 4개의 원자와 결합하고 있었습니다. 그럼 12개중 4개는 나왔지요. 나머지 8개가 남았는데 A 원자 위로 4개가 올라갔습니다. 그렇다면 나머지 4개는 A의 반대편 아래쪽으로 결합하고 있을겁니다. 어느 한쪽으로 7개 있고 반대편에 1개 있을수도 있지 않냐는 비대칭 구조는 여기서는 무리입니다.. -_- (111) 면의 경우도 아주 간단하죠. A 원자 주위로 6개가 보였으니, 나머지 6개가 남았습니다. 그럼 자연스럽게 위쪽에 3개, 아래쪽으로 3개를 예상할 수 있습니다. 그렇다면 마찬가지로 (110)면의 경우에도 적용하면, A 원자 좌우로 하나씩 2개가 결합한게 보이죠. 그럼 남은건 10개겠고, 대칭이 되어야 하니까 A 원자 위쪽으로 5개, A원자 아래쪽으로 5개가 위치할겁니다. 그렇게 비록 위치는 정확히 알 지 못하더라도 몇개가 결합하고 있나 정도는 당연스럽게 파악할 수 있습니다. 그리고 이런 꼼수는 교과서에는 안나옵니다. 학교에서 이렇게 가르쳐주는 경우가 있는지는 모르겠지만, 이건 배우는게 아니라 FCC 몇번 그리다보면 아 이렇구나 하고 그냥 알게되는 부분입니다.. - _- 많은 경우, 학생들이 원자들의 위치를 이해하기 여려워 하는것은 수업중에 단지 FCC(Face Centered Cubic), BCC(Body Centered Cubic), HCP(Hexagonal Close Packed) 라는 결정구조의 unit cell 하나의 모습만 가르쳤기 때문이라 생각합니다. 결정이란 것은 수많은 unit cell의 모임이기 때문에, 그것을 여러개 이어붙인 전체적인 모습으로 이해해야 하는 것이지 그냥 unit cell 하나로 이해할 수가 있는 것이 아니거든요. 어쨌거나 뭐 그렇습니다 -_ -

우햐튼 (110) 면에서는 이렇게 놓인다.
A원자 주위로 먼저 4개가 위치하고 그 한가운데로 1개가 올라감. 5개 모두 A 원자와 닿아있다.
그래서 어쨌든.. (110)면에서 표면 원자는 5개의 끊어진 결합이 존재하고, 원자 하나당 표면에너지는 (ε/2 x 5) 입니다. 다른 면들의 원자들과 비교해보면 제일 높은 에너지를 갖고있는데, 표면에서 보이는 원자들의 수가 적으면 적을 수록 표면에너지가 높아진다는 것을 알 수 있습니다. FCC가 아닌 BCC나 HCP 로 결정구조가 다르면 같은 면이라도 원자의 위치와 갯수가 다르기 때문에 표면에너지도 달라지게 되겠지요.
표면에너지란 것은 결국 원자들 간의 결합에너지 입니다. 그래서 원자간의 결합력이 강한 물질일수록 표면에너지가 높은 경향이 있습니다. 이것은 물질의 녹는점(melting point)이 높은 물질일수록 표면에너지가 높다는 것을 말해주죠. 녹는점이 높다는 것은 결합을 끊기가 그만큼 어렵다는 의미입니다. 또한, 표면에너지는 본래는 다른 원자와 결합해야 하는 에너지인데, 결합을 못해서 남아도는 여분의 에너지 입니다. 그런데 모든 물질은 에너지가 낮을수록 안정하기 때문에 표면적을 축소시키거나 표면원자가 대기중의 수분이나 먼지, 기체등과 흡착 하거나 결합하여 에너지를 가능한 낮추려는 성질이 있습니다. 이런 표면에너지의 존재는 애써서 금방 닦은 표면이 오염되거나, 금속 표면이 쉽게 부식되는 이유이기도 하며, 스퍼터링시 기판표면에 박막을 입힐 수 있는 이유 중 하나이기도 합니다. 우리는 수많은 물질의 표면 특성을 제어하기 위해 엄청난 노력과 비용을 들이고 있습니다. 닦고, 기름치고, 계면활성제를 바르고, 코팅하고, 산화막을 입히거나 제거하고, 박막을 입히는 등.. 그렇게 표면 특성을 제어한다는 것은 바로 표면에너지와의 싸움입니다.
* 위 방법으로 계산된 표면에너지는 단일원소로 이루어진 순금속의 최외각층의 원자만 고려한 것입니다. 만약 이온결합 물질이라면 각 방향의 전기적인력이 미치는 거리까지를 모두 계산해야 하기 때문에 복잡해집니다.
표면에너지 확장판 보러가기 -> 여기클릭 -_ -
...by 개날연..
어째 오늘 내용은 무슨 재미없는 강의시간 같군요 -_ -
앞으로 이런식의 이야기 전개는 피해야 하겠습니다. - _-
바다가서 비키니도 한번 못봤는데 여름이 끝나고 있습니다..;ㅁ;
글 : 개날라리연구원
그림 : 개날라리연구원
업로드 : 개날라리연구원
발행한곳 : 개날라리연구소
........ - _-y~
'플라즈마와 박막프로세스 > 박막의 특성과 측정' 카테고리의 다른 글
| 박막 표면의 불순물 #2. (63) | 2013.02.07 |
|---|---|
| 박막 표면의 불순물 #1. (48) | 2012.11.13 |
| 밀착력에 영향을 주는 것들 (40) | 2012.09.24 |
| 박막의 밀착력(Adhesion) (85) | 2012.09.16 |
| 표면(Surface)이란? (17) | 2012.08.15 |